Lejearrangement - Rapporten - Styrkelære - Akselberegning - Tolerancer - Materialelære - Robot - Gokartberegning - Pladeklip

 

Maskinteknik A

Eksempel på styrkeberegning af en aksel.

Denne aksel anvendes til et lejearrangement til en rulletrappe. Den belastes på midten med en kraft på 2800 [N]. Omløbshastigheden n = 630 [O/min]. Levetiden på kuglelejer ønskes L_10h = 4000 [timer]. Kuglelejets indre diameter ønskes 17 [mm]. Udfra disse data kan kuglelejernes størrelse findes (find C/P værdi i kuglelejekatalog).

C/P = 5,32 og med en lejereaktion (se nedenfor) på 1400 [N] findes det dynamiske bæretal C = 1400[N] ∙ 5,32 = 7.448 [N].
Så kan et "Enraded sporkugleleje" SKF 6203 anvendes, check først indbygningsforholdene, olietætningsring dimensioner, dæksel mm.

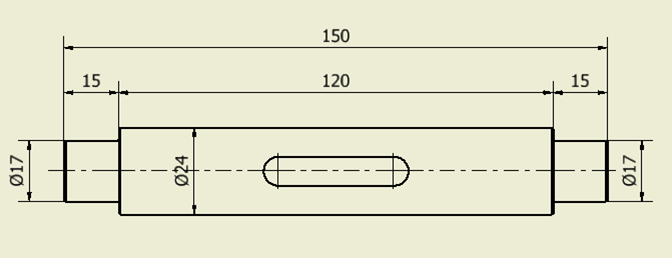
Beregning af kræfter og lejereaktioner, og bøjningsmoment. For nemheds skyld er lejereaktioner vist på akselenderne. Reaktionerne kan evt. vises midt på 15 mm aksel-stykket, så bliver bøjningsmomentet lidt mindre.

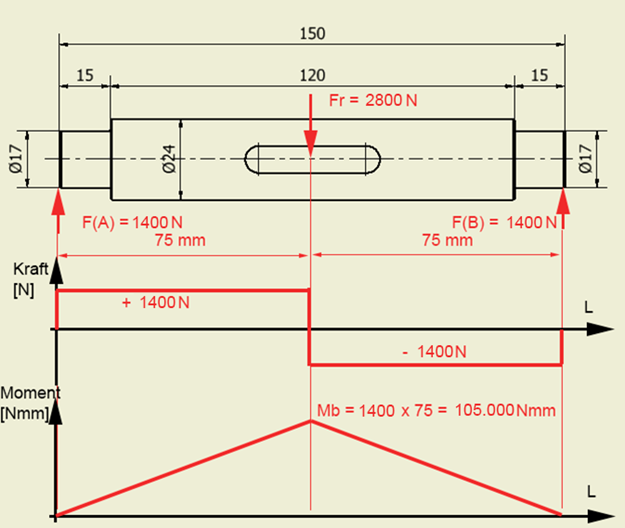
Tværkraftkurve og momentkurve herover.

 

Akslens modstandsmoment på midten af akslen, lidt tilnærmet (når man ikke medregner noten, se også senere):

W_x = W_y = π/32 ∙ d³ = π/32 ∙24³ = 1.357 mm³

 

Bøjningsmomentet beregnes til:

Mb = 1400 [N]∙ 75 [mm] = 105.000 [N∙mm]

Bøjningsspændingerne beregnes til:

Bøjningsspænding

σ_b = M_b/W_x ≤  σ_{b till}

σ_b bøjningsspænding i [MPa].

M_b = momentet , enhed [N∙mm], W_x = modstandsmomentet, enhed [mm³]

σ_b = M_b/W_x = 105.000 [N∙mm] / 1.357 [mm³] = 77,4 [MPa]

 

Man kan også bruge Inventor til at beregne Inertimoment I_x og herefter modstandsmoment W_x. Optegn blot en cirkel med samme diameter som akslen. Brug en funktion "Region Properties" til at udregne inertimomenter.

   

Area Moments of Inertia with respect to Principal Axes(mm^4):
I_x = I_y = 16.286,016 [mm⁴]

W_x = I_x / (d/2) [mm³] = 16.286/12 = 1.357 [mm³]

σ_b = M_b / W_x = 105.000 [N∙mm] / 1.357 [mm³] = 77,4 [MPa]

 

Hvis noten medregnes findes: Indtegn noten på cirklen.

   

Area Moments of Inertia with respect to Principal Axes(mm^4):
I_x = 13.083,745 [mm⁴]

I_y = 16.132,77 [mm⁴]

W_x = I_x / (d/2) [mm³] = 13.083/12 = 1.090 [mm³]

σ_b = M_b / W_x = 105.000 [N∙mm] / 1.090 [mm³] = 96,3 [MPa]

Valg af materiale.

Hvis der overslagsmæssigt regnes på konstruktionen som en roterende maskine med vekslende belastning, kan de tilladelige bøjningsspændinger for materialerne "maskinstål":

S235 (st37-2) med R_mt på 360 [MPa] sættes til σ_{b till} = 65 [MPa], og for

S355 (st50-2) med R_mt på 490 [MPa]) til σ_{b till} = 85 [MPa], og for

st70-2 med R_mt på 690 [MPa]) til σ_{b till} = 115 [MPa].

( I flg. "Teknisk Styrkelære, Preben Madsen, 2.udgave 2003).

Dvs. akslen bør fremstilles i st70-2 maskinstål. Der er således en rimelig stor sikkerhedsfaktor på disse beregninger. Evt. S3555, med lidt mindre sikkerhedsfaktor dog.

Se også her: http://apv.otg.dk/maskinstyrkelaere.html#M

  

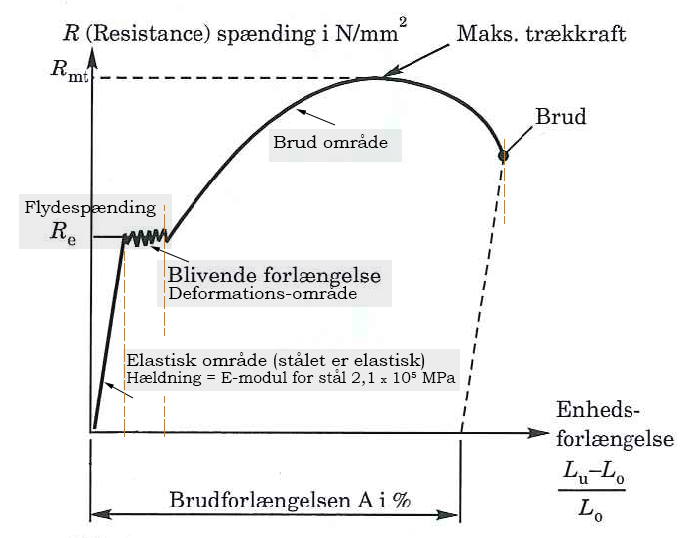
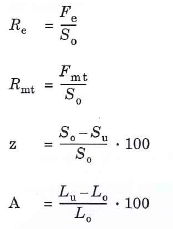
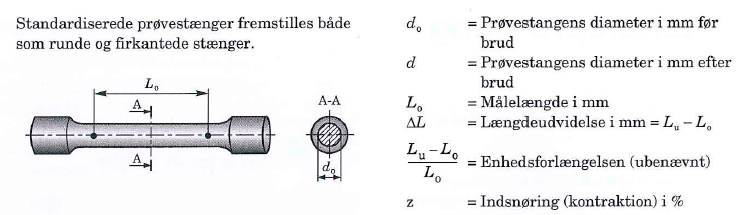
R_e (og F_e ) er den spænding målt i [MPa] der betyder at stangen begynder at deformeres (flydespændingen). Max. trækstyrke R_mt er max. trækspænding i [MPa] der får stangen til at brydes over i to dele. I praksis trækkes i stangen med en given kraft F, og så deles kraften med tværsnittets areal S_o for at finde materialespændingerne.
Arealet er S_o = π/4 ∙ d_o².