Lejearrangement - Rapporten - Styrkelære - Akselberegning - Tolerancer - Materialelære - Robot - Gokartberegning - Pladeklip
Maskinteknik A
Styrkelæren tager udgangspunkt i fysik og statik, og hvordan et emne/konstruktion påvirkes eller belastes af kræfter. Derfor findes der fx på HTX et fag der hedder "Statik og styrkelære", hvor man lærer om sammenhængen mellem de to områder. Statikken giver kræfterne, størrelsen og retningen, mens styrkelæren bruges til at bestemme størrelsen på de forskellige dimensioner i en konstruktion. På den måde kan delene dimensioneres, og størrelsen på aksler, stænger, rør, bolte, godstykkelser osv kan bestemmes.
Så det første man skal finde ud af er, altså hvilke kræfter der virker og hvor store de er. Desuden også hvordan en kraft opfører sig, om den er er 1) rolig og stillestående, om den er 2) varierende eller påvirkningen er en 3) vekslende belastning. Se figurerne herunder.
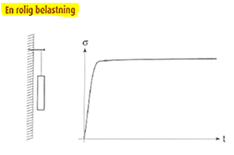
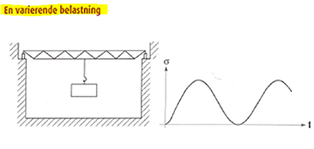
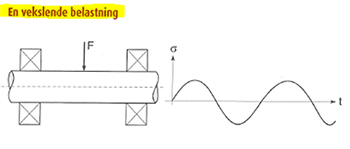
Desuden er materialevalget vigtigt for dimensioneringen, da fx stål, aluminium og plast har forskellig "indre" styrke - se senere ↓.
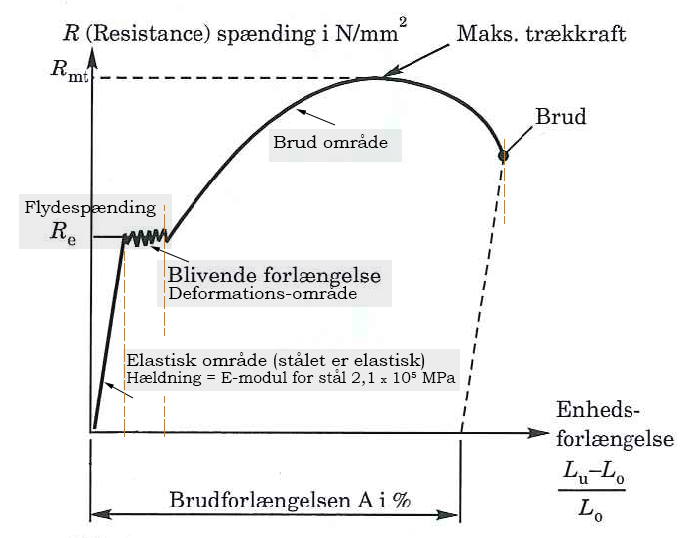
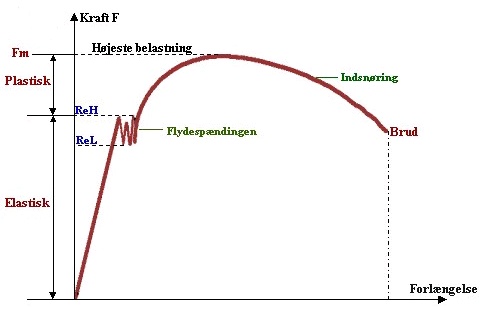
Udgangspunktet for stål's styrke er et trækdiagram - hvor man ved en trækprøve finder ud af hvor stor en kraft materialet kan modstå, inden det ødelægges. Herunder vises hvordan trækdiagrammet for stål ser ud.
Der er ligesom tre områder.
Først det elastiske område, hvor stålet opfører sig lidt som en elastisk fjeder. Materialet forlænges ved træk og får sin oprindelige længde igen, når man slipper.
Næste område er når flydespændingen overskrides, så begynder materialet så småt at gå i stykker. Molekylerne i materialet kan ikke længere holdes sig på plads (metalbindingerne skrider). Der opstår en blivende forlængelse, og emnet får ikke længere sin oprindelige længde når man slipper.
Tredje fase opstår ved yderligere træk-belastning, hvor stangen bliver meget længere, og til trækkes over i to dele. Nu er materialet helt ødelagt.
Det gælder altså om at holde sig under flydespændingen, og helst med en god sikkerhedsfaktor. Hvis konstruktionen belastes lige til flydespændingen risikerer man jo at den bliver ødelagt. Sikkerhedsfaktoren skal måske være 2, 3 eller mere, således at man holder sig noget under flydespændingen. I mange konstruktioner fx byggekraner eller bygninger af stål er der nøje regler for udregning og dimensionering, og som skal overholdes. Det lærer man om fx i faget "Statik og styrkelære" på htx, eller senere på ingeniørstudiet på universitetet.
Diagrammet her viser altså spændingen Rmt, hvor spændingen er kraften F målt i [N] divideret med tværsnitsarealet målt i [mm2]. Enheden kaldes også MPa (MegaPascal som jo egentlig er en tryk-enhed). Og de tilladelige spændinger for et materiale måles i denne enhed.
Formler der især bruges til at beskrive sammenhængen ved trækprøvning:
| Tøjning: | Ԑ = ∆L/L o forholdet mellem stangens forlængelse og den oprindelige længde (Lu-Lo)/Lo. |
| Hookes lov: | δ = Ԑ ∙ E (Tøjning ∙ Elasticitetsmodulet), hvor E for stål er 2,1∙105 MPa, og gælder i det elastiske område på trækprøvediagrammet. Dvs. det er en ret linje og stålet opfører sig som en elastisk fjeder. |
| Forlængelse: | Forlængelse af stangen måles på trækprøveapparatet Lu - Lo. Eller kan beregnes med formlen |
Trækdiagram med F (trækkraften) på y-aksen. Når man skal bukke/bøje et stål-emne, skal man tilføje en kraft der svarer til flydespændingen eller lidt højere, ellers vil emnet gå tilbage til sin oprindelige facon. Så ved bukkeprocesser og valseprocesser skal man op på flydespændingen, inden emnet får en ny facon.
Flydespændingsområdet har ofte en øvre ReH og en nedre ReL flydespænding. Så vil man, ved styrkeberegning, i givet fald anvende den nedre værdi, så man er på den sikre side.
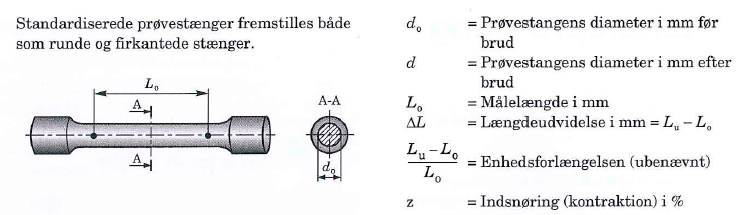
Trækprøvestang til at måle stålets styrke er vist herunder. Stangen sættes op i en trækprøve-stand, og belastes med en trækkraft, der stiger langsomt indtil den knækker (trækkes) over i to dele. Se herunder de forskellige betegnelser for stangens dimensioner.
Grundlæggende styrkelære
Forskellige belastninger som kan opstå i en given konstruktion kan være disse: Træk, tryk, bøjning, forskydning, torsion.
Trækkraft. Der trækkes i konstruktionen (materialet).
Trykkraft i konstruktionen.
Bøjning i konstruktionen.
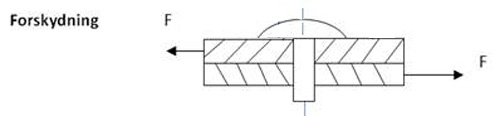
Forskydningskraft - kaldes også overklipningskraft. Fx på en skrue eller nitte.
Torsion
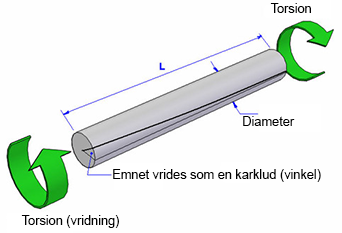
Kaldes også vridning. Det opstår fx når vi bruger en skruetrækker på en skrue (som at vride en karklud).
Der er ofte torsion i en aksel. Hvis akslen har forbindelse til en motor eller hvis der er monteret et tandhjul eller lignende.
Tilladelige trækspændinger ved overslagsberegninger, afhængig af belastningens karakter.
Spændingerne angives i MPa (Fra Statik og styrkelære 3. udg., Preben Madsen, Praxis),
Materiale |
Belastningens karakter |
|
||
|
Rolig |
Varierende |
Vekslende |
Flydespændingen |
St 37-2 (S235) |
125 |
80 |
60 |
235 |
St 50-2 (S355) |
175 |
115 |
80 |
355 |
St 70-2 |
260 |
170 |
115 |
|
Aluminium (AlSi 7 Mg) |
155 |
85 |
60 |
240 |
Bronze, messing (CuZn 15) |
125 |
100 |
80 |
220 |
Nylon (Pa 6) |
55 |
35 |
20 |
85 - 45 |
Tilladelige trykspændinger. Spændingerne angives i MPa (Fra Statik og styrkelære),
Materiale |
Belastningens karakter |
|
||
|
Rolig |
Varierende |
Vekslende |
Flydespændingen |
St 37-2 (S235) |
125 |
80 |
60 |
235 |
St 50-2 (S355) |
175 |
115 |
80 |
355 |
St 70-2 |
260 |
170 |
115 |
|
Aluminium (AlSi 7 Mg) |
155 |
85 |
60 |
240 |
Bronze, messing (CuZn 15) |
125 |
100 |
80 |
220 |
Nylon (Pa 6) |
55 |
35 |
20 |
85 - 45 |
Tilladelige forskydningspændinger
Materiale |
Belastningens karakter |
|
||
|
Rolig |
Varierende |
Vekslende |
Flydespændingen |
St 37-2 (S235) |
100 |
65 |
48 |
235 |
St 50-2 (S355) |
140 |
90 |
65 |
355 |
St 70-2 |
210 |
135 |
90 |
|
Aluminium (AlSi 7 Mg) |
140 |
65 |
50 |
240 |
Bronze, messing (CuZn 15) |
110 |
80 |
60 |
220 |
Nylon (Pa 6) |
45 |
30 |
15 |
85 - 45 |
Tilladelige bøjningspændinger
Materiale |
Belastningens karakter |
|
||
|
Rolig |
Varierende |
Vekslende |
Flydespændingen |
St 37-2 (S235) |
140 |
85 |
65 |
235 |
St 50-2 (S355) |
185 |
125 |
85 |
355 |
St 70-2 |
285 |
185 |
115 |
|
Aluminium (AlSi 7 Mg) |
185 |
80 |
60 |
240 |
Bronze, messing (CuZn 15) |
115 |
85 |
65 |
220 |
Nylon (Pa 6) |
- |
- |
- |
- |
Tilladelige torsionspændinger
Materiale |
Belastningens karakter |
|
||
|
Rolig |
Varierende |
Vekslende |
Flydespændingen |
St 37-2 (S235) |
80 |
50 |
37 |
235 |
St 50-2 (S355) |
105 |
70 |
50 |
355 |
St 70-2 |
160 |
105 |
75 |
|
Aluminium (AlSi 7 Mg) |
95 |
55 |
35 |
240 |
Bronze, messing (CuZn 15) |
55 |
35 |
20 |
220 |
Nylon (Pa 6) |
- |
- |
- |
- |
Tilladelige fladetryk
Materiale |
Belastningens karakter |
|
||
|
Rolig |
Varierende |
Vekslende |
Flydespændingen |
St 37-2 (S235) |
100 |
75 |
40 |
235 |
St 50-2 (S355) |
120 |
95 |
60 |
355 |
|
|
|
|
|
Aluminium (AlSi 7 Mg) |
60 |
45 |
25 |
240 |
Bronze, messing (CuZn 15) |
55 |
42 |
35 |
220 |
Nylon (Pa 6) |
35 |
30 |
15 |
85 - 45 |
Kræfter og momenter

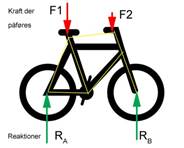 Konstruktionen optegnes grafisk (en principskitse) og de kræfter der virker skal påføres. Ud fra ligevægtsbetragtninger kan reaktioner (kraften) og momenter bestemmes.
Konstruktionen optegnes grafisk (en principskitse) og de kræfter der virker skal påføres. Ud fra ligevægtsbetragtninger kan reaktioner (kraften) og momenter bestemmes.
For at finde ud af hvilke dimensioner og materialer der skal bruges, omregnes kræfterne til materialespændinger, hvorefter et tværsnit på en aksel eller bjælke kan bestemmes.
Hertil bruges både enten arealet, inertimoment og modstandsmomentet. Se næste side.
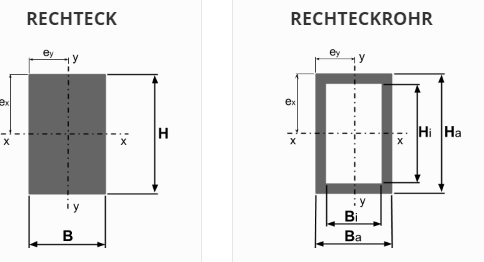
Beregn modstandsmomenter for forskellige profiler:
https://www.online-berechnung.at/widerstandsmoment-traegheitsmoment.html
Eksempel på et tværsnit og beregning af det tilhørende modstandsmoment. For firkant-rør og for et rundt rør.
Inertimoment og modstandsmoment for kvadratisk rør
Areal:
Inertimoment:
Modstandsmoment:
Afstand e:
Inertimoment og modstandsmoment for rundt rør
Areal:
Inertimoment:
Modstandsmoment:
Inertimomenter og modstandsmomenter for forskellige tværsnit - generelt
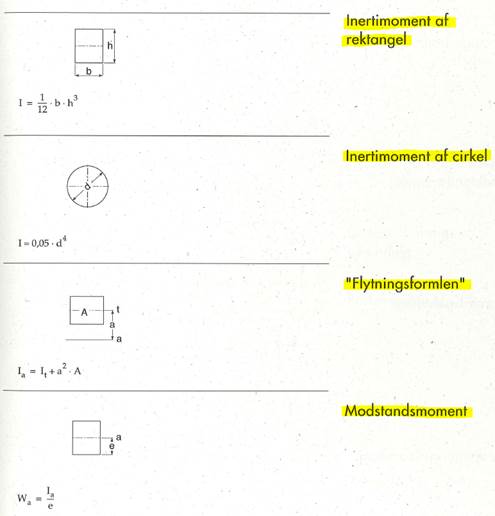
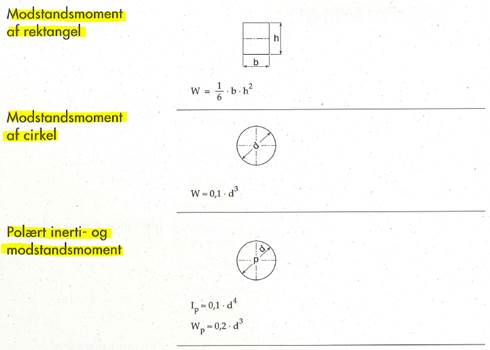
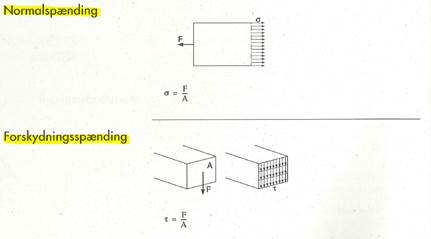
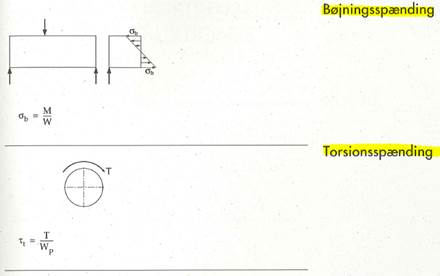
Spændinger
|
|
|
|
Sammensatte spændinger (Von Mises spændinger – se Inventor-eksempel senere).
Ofte vil der være forskellige spændinger i en konstruktion.
Træk/tryk- og bøjningsspændinger kan lægges sammen:
σo = σ + σb
Hvis der samtidig er torsionsspænding:
![]()
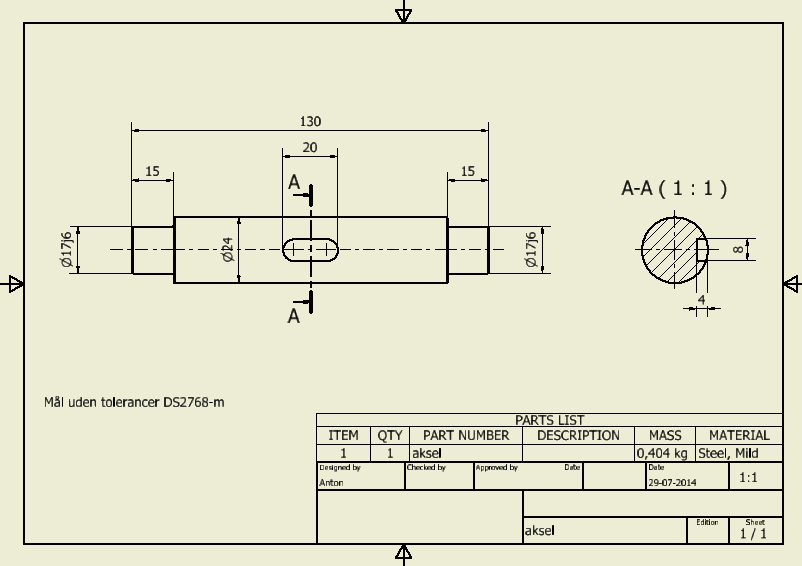
Stressanalyse med Inventor
Brug tegning herunder aksel.ipt.
Vælg ”Environments” og ”Stress Analysis”, og ”Create Simulation”.
Klik på ”Fixed Constraint” og klik på aksel-enderne, hvor kuglelejer skal monteres.
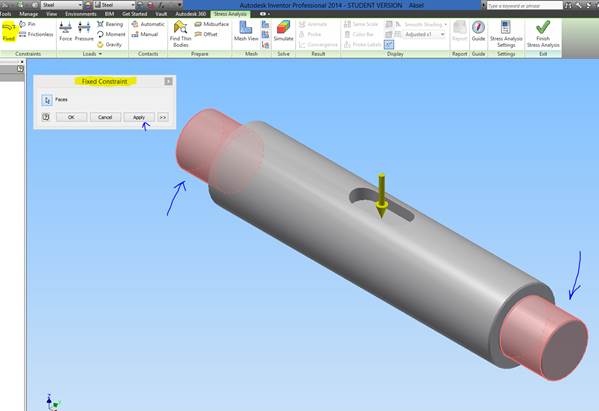
Herefter påføres en kraft fx F=1000[N]
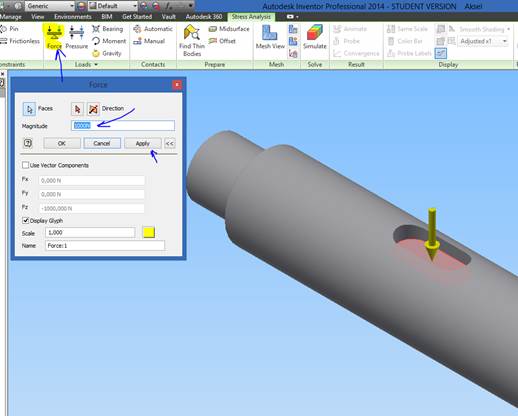
Klik på ”Simulate” og kør en simulation.
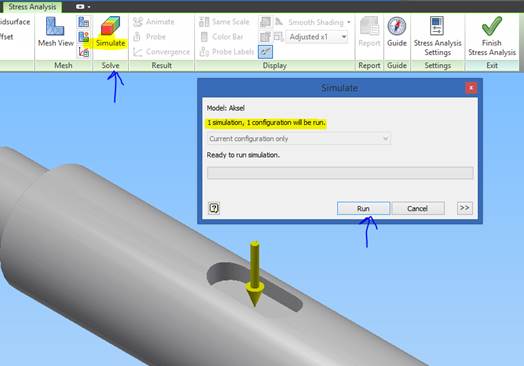
Resultatet af stressanalysen vises (”Von Mises”- stress giver de sammensatte spændinger, der kan fx være træk/tryk, forskydning og bøjning samtidigt).
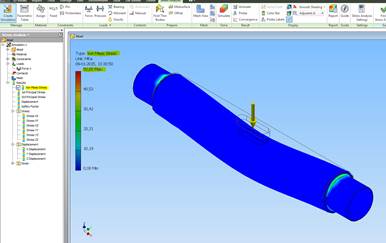
Max. spændinger ses ved diameterovergangen. Max. ca. 50,65 MPa (MegaPascal ≈ N/mm2).
Hvis man ser på spændinger “Z”-planet giver det noget mindre spændinger. Max. 14,36 MPa.
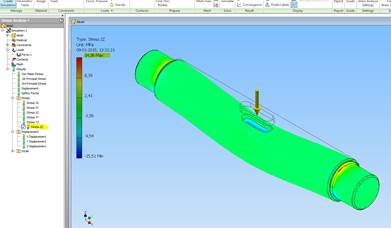
Nedbøjningen i z-retningen (z-displacement) kan bestemmes.
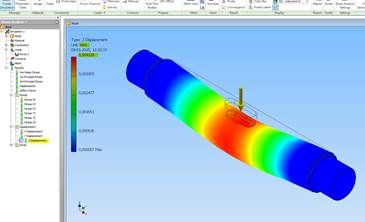
Max. nedbøjning findes til 0,00412 [mm].